Y Coordinate Definition Math
adminse
Apr 01, 2025 · 8 min read
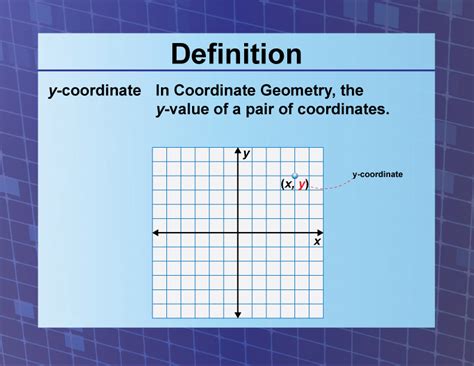
Table of Contents
Decoding the Y-Coordinate: A Deep Dive into its Mathematical Definition and Applications
What if our understanding of space and location hinged entirely on grasping the concept of the y-coordinate? This fundamental element of coordinate geometry underpins countless applications across diverse fields, from mapping and navigation to advanced physics and computer graphics.
Editor’s Note: This article on the y-coordinate definition in mathematics provides a comprehensive exploration of this critical concept, including its historical context, practical applications, and relevance in various fields. We aim to offer a clear and accessible understanding for students, researchers, and anyone curious about the power of coordinate systems.
Why the Y-Coordinate Matters: Relevance, Practical Applications, and Industry Significance
The y-coordinate, a seemingly simple numerical value, is a cornerstone of analytical geometry and its applications. It represents the vertical position of a point in a two-dimensional coordinate system, providing essential information about location and spatial relationships. Its importance extends far beyond basic mathematics, finding critical applications in:
-
Cartography and Geographic Information Systems (GIS): Y-coordinates, often paired with x-coordinates and sometimes z-coordinates (for elevation), form the basis of location data used in maps, GPS systems, and spatial analysis. Accurate representation of location relies entirely on the precise definition and use of these coordinates.
-
Computer Graphics and Game Development: The visual representation of objects on computer screens hinges on coordinate systems. The y-coordinate dictates the vertical position of every pixel, vertex, or object in a game or graphic, defining its placement and rendering.
-
Engineering and Design: In fields like civil, mechanical, and electrical engineering, coordinate systems are essential for designing structures, circuits, and machinery. The y-coordinate aids in precise positioning of components and ensuring the correct spatial relationships between them.
-
Physics and Data Visualization: In physics, coordinate systems are used to model motion, forces, and fields. The y-coordinate plays a vital role in defining trajectories, calculating vectors, and visualizing data related to vertical displacement or forces.
Overview: What This Article Covers
This article will delve into the core aspects of the y-coordinate definition, exploring its historical context, its relationship to the x-coordinate, different coordinate systems utilizing the y-coordinate (like Cartesian and polar coordinates), and its wide-ranging applications. Readers will gain a deeper understanding of this fundamental mathematical concept and its impact across diverse fields.
The Research and Effort Behind the Insights
This article draws upon established mathematical literature, textbooks on coordinate geometry and analytical geometry, and resources from reputable online academic sources. The information presented aims to be accurate and easily understandable, supporting claims with clear explanations and examples. The structured approach ensures a logical flow of information, facilitating a comprehensive understanding of the y-coordinate.
Key Takeaways: Summarize the Most Essential Insights
-
Definition and Core Concepts: A precise definition of the y-coordinate within the Cartesian coordinate system and its role in specifying location.
-
Relationship to the X-Coordinate: The interplay between the x- and y-coordinates in defining a point's location and their use in various equations and calculations.
-
Coordinate Systems Employing Y-Coordinates: Exploration of Cartesian, polar, and other coordinate systems that incorporate the y-coordinate and how their usage differs.
-
Applications across Disciplines: Examination of the diverse applications of y-coordinates in fields such as mapping, computer graphics, and physics.
Smooth Transition to the Core Discussion
Having established the significance of the y-coordinate, let's now delve into its core definition and explore its multifaceted role in mathematics and beyond.
Exploring the Key Aspects of the Y-Coordinate
Definition and Core Concepts:
In a two-dimensional Cartesian coordinate system, the y-coordinate represents the vertical distance of a point from the x-axis. The x-axis is the horizontal reference line, and the y-axis is the vertical reference line. These two axes intersect at a point called the origin (0,0). A point's position is uniquely determined by its x-coordinate (horizontal distance from the y-axis) and its y-coordinate (vertical distance from the x-axis), written as an ordered pair (x, y). A positive y-coordinate indicates a point above the x-axis, while a negative y-coordinate indicates a point below the x-axis.
Relationship to the X-Coordinate:
The x- and y-coordinates work in tandem to define the precise location of a point in a 2D plane. They are independent yet interdependent. One cannot define a point's location accurately without both coordinates. The relationship between x and y can be expressed through various mathematical equations, like the equation of a line (y = mx + c), where 'm' is the slope and 'c' is the y-intercept. These equations define how x and y values are related within a specific geometric context.
Coordinate Systems Employing Y-Coordinates:
-
Cartesian Coordinates: This is the most common coordinate system, using perpendicular x and y axes.
-
Polar Coordinates: In this system, a point is defined by its distance from the origin (r) and the angle (θ) it makes with the positive x-axis. The y-coordinate can be derived from the polar coordinates using the formula: y = r * sin(θ).
-
Other Coordinate Systems: Three-dimensional coordinate systems (like Cartesian in 3D, cylindrical, and spherical) extend the concept further, adding a z-coordinate to represent depth. The y-coordinate retains its importance representing vertical position, now within a three-dimensional space.
Applications Across Disciplines:
-
Mapping and GIS: Latitude and longitude are essentially spherical coordinates, with latitude analogous to the y-coordinate, indicating the position north or south of the equator.
-
Computer Graphics: Every pixel on a screen is assigned an (x,y) coordinate pair, enabling the precise placement of visual elements.
-
Physics: Projectile motion, for instance, utilizes the y-coordinate to model the vertical displacement of an object under the influence of gravity. Force vectors are also often defined using x and y components.
Closing Insights: Summarizing the Core Discussion
The y-coordinate is more than a simple number; it's a fundamental building block for representing location and spatial relationships in two and three dimensions. Its applications are vast and essential to various fields, highlighting its importance in mathematics and beyond. A strong understanding of the y-coordinate is crucial for anyone working with spatial data, graphics, or physical systems.
Exploring the Connection Between Linear Equations and the Y-Coordinate
The y-coordinate plays a crucial role in understanding and representing linear equations. Linear equations, which describe straight lines, often take the form y = mx + c, where 'm' is the slope and 'c' is the y-intercept.
Key Factors to Consider:
-
Roles and Real-World Examples: The y-intercept (c) in the equation y = mx + c directly represents the y-coordinate where the line intersects the y-axis. This is a critical point for understanding the line's position and behavior. For example, in economics, a linear equation might model the relationship between price (y) and quantity (x), and the y-intercept would represent the price when the quantity is zero.
-
Risks and Mitigations: Misinterpreting the y-intercept or the slope in a linear equation can lead to incorrect conclusions. Careful analysis of the data and the context is crucial to avoid misinterpretations.
-
Impact and Implications: Linear equations and their reliance on the y-coordinate are fundamental tools for modeling relationships between variables in various fields, from physics to finance.
Conclusion: Reinforcing the Connection
The strong connection between linear equations and the y-coordinate emphasizes the y-coordinate's fundamental role in representing and analyzing linear relationships. Understanding this relationship is key to applying linear models effectively across diverse fields.
Further Analysis: Examining the Y-Intercept in Greater Detail
The y-intercept, the point where a line intersects the y-axis, is particularly insightful. It represents the value of y when x is zero, providing crucial information about the relationship described by the linear equation.
FAQ Section: Answering Common Questions About the Y-Coordinate
-
What is the y-coordinate? The y-coordinate is the vertical position of a point in a two-dimensional coordinate system, measured relative to the x-axis.
-
How is the y-coordinate used in graphing? The y-coordinate, along with the x-coordinate, specifies the location of a point on a graph, enabling the plotting of data and visualization of functions.
-
What is the difference between the x-coordinate and the y-coordinate? The x-coordinate represents horizontal position, while the y-coordinate represents vertical position.
-
Can the y-coordinate be negative? Yes, a negative y-coordinate indicates a point below the x-axis.
-
How is the y-coordinate used in three-dimensional space? In three-dimensional space, the y-coordinate still represents the vertical position, but it's one component of a three-coordinate system (x, y, z).
Practical Tips: Maximizing the Benefits of Understanding Y-Coordinates
-
Practice plotting points: Practice plotting points on a Cartesian plane to develop a strong understanding of the relationship between x and y coordinates.
-
Analyze linear equations: Learn to identify the slope and y-intercept in linear equations, and understand how these values affect the line's position and slope.
-
Explore different coordinate systems: Familiarize yourself with polar and other coordinate systems to understand the diverse ways in which location can be represented.
Final Conclusion: Wrapping Up with Lasting Insights
The y-coordinate, seemingly simple, serves as a fundamental building block for understanding space, location, and linear relationships. Its applications are boundless, from mapping our world to creating the digital landscapes we interact with daily. A solid grasp of the y-coordinate definition and its usage is crucial for success in various academic and professional domains. Its significance extends far beyond basic mathematics, playing a vital role in shaping our understanding of the world around us.
Latest Posts
Latest Posts
-
Is Liquidity Mining Profitable
Apr 03, 2025
-
Is Liquidity Mining Safe
Apr 03, 2025
-
How Does Liquidity Mining Work
Apr 03, 2025
-
What Is Binance Liquidity Mining
Apr 03, 2025
-
What Is Eth Liquidity Mining
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Y Coordinate Definition Math . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.