Definition Y Intercept
adminse
Apr 01, 2025 · 8 min read
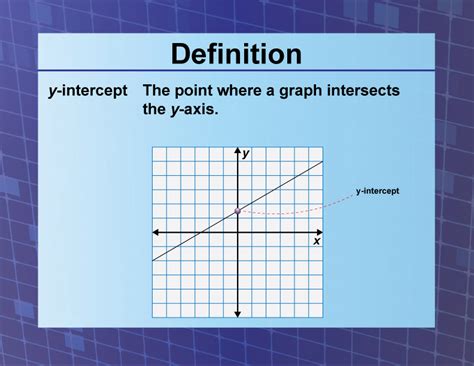
Table of Contents
Unlocking the Secrets of the Y-Intercept: A Comprehensive Guide
What if a single point held the key to understanding the behavior of an entire line? The y-intercept, that seemingly simple point, is far more powerful than it initially appears, providing crucial insights into linear relationships across diverse fields.
Editor’s Note: This article on the y-intercept provides a comprehensive exploration of its definition, applications, and significance in various mathematical and real-world contexts. Updated with the latest information, this resource aims to offer a clear and insightful understanding of this fundamental concept.
Why the Y-Intercept Matters: Relevance, Practical Applications, and Industry Significance
The y-intercept, a seemingly simple concept, holds immense significance in mathematics, statistics, and numerous real-world applications. It represents the point where a line intersects the y-axis – the vertical axis on a Cartesian coordinate plane. Understanding the y-intercept is crucial for interpreting linear relationships, making predictions, and solving problems across diverse fields, including:
- Economics: Modeling supply and demand, analyzing cost functions, and predicting market trends.
- Finance: Forecasting investment returns, understanding loan amortization, and analyzing financial growth.
- Engineering: Designing structures, analyzing circuits, and modeling physical systems.
- Physics: Analyzing motion, understanding forces, and modeling various physical phenomena.
- Data Science: Interpreting regression models, understanding trends in data, and making data-driven decisions.
Overview: What This Article Covers
This article provides a comprehensive overview of the y-intercept, covering its definition, calculation, significance in different contexts, and applications in diverse fields. Readers will gain a solid understanding of its theoretical underpinnings and its practical implications, along with various examples to solidify comprehension.
The Research and Effort Behind the Insights
This article draws upon established mathematical principles, extensively researched examples from various fields, and a structured approach to ensure clarity and accuracy. The information presented is supported by widely accepted mathematical concepts and real-world applications, ensuring that readers receive reliable and trustworthy information.
Key Takeaways: Summarize the Most Essential Insights
- Definition and Core Concepts: A precise definition of the y-intercept and its representation in various forms.
- Calculation Methods: Different approaches to calculating the y-intercept, including using the slope-intercept form, point-slope form, and solving systems of equations.
- Interpreting the Y-Intercept: Understanding the meaning and significance of the y-intercept in different contexts, including its relationship to the slope and the overall linear equation.
- Real-World Applications: Examining how the y-intercept is applied in various fields to analyze data, make predictions, and solve practical problems.
- Advanced Applications: Exploring more complex scenarios where understanding the y-intercept is crucial, such as in multivariable calculus and statistical modeling.
Smooth Transition to the Core Discussion
Having established the importance of understanding the y-intercept, let's delve into its core aspects, exploring its calculation, interpretation, and applications in detail.
Exploring the Key Aspects of the Y-Intercept
1. Definition and Core Concepts:
The y-intercept is the point where a line crosses the y-axis. This point always has an x-coordinate of 0. It's typically represented as (0, b), where 'b' is the y-coordinate and represents the value of the dependent variable when the independent variable is zero. In the slope-intercept form of a linear equation, y = mx + b, 'b' specifically represents the y-intercept.
2. Calculation Methods:
Several methods can be used to determine the y-intercept:
-
Slope-Intercept Form (y = mx + b): If the equation of a line is in this form, the y-intercept 'b' is directly visible.
-
Point-Slope Form (y - y1 = m(x - x1)): Substitute x = 0 and solve for y. The resulting y-value is the y-intercept.
-
Two-Point Form: If two points on the line are known, find the slope (m) using the formula m = (y2 - y1) / (x2 - x1). Then, use the point-slope form with one of the points to determine the equation of the line and subsequently find the y-intercept.
-
Solving Systems of Equations: If the line is defined as part of a system of equations, solve the system to find the coordinates of the intersection point. If the intersection point lies on the y-axis (x = 0), the y-coordinate represents the y-intercept.
3. Interpreting the Y-Intercept:
The interpretation of the y-intercept depends heavily on the context of the problem. In a simple linear equation representing a physical relationship, the y-intercept often represents the initial value or starting point. For instance:
-
Cost Function: In a cost function, where y represents the total cost and x represents the number of units produced, the y-intercept represents the fixed costs (costs incurred even when no units are produced).
-
Distance-Time Graph: In a distance-time graph, the y-intercept represents the initial distance from the origin at time zero.
-
Temperature-Time Graph: In a temperature-time graph, it might represent the initial temperature.
4. Applications Across Industries:
The y-intercept finds applications in numerous fields:
- Economics: Determining fixed costs in a cost function or the initial demand at a price of zero.
- Finance: Finding the initial investment value in a compound interest calculation or the initial balance in a loan amortization schedule.
- Engineering: Establishing initial conditions in system modeling or determining a baseline value in sensor readings.
- Science: Representing initial values in experiments or setting reference points in measurements.
5. Impact on Innovation:
The y-intercept is a fundamental concept that underpins many advanced mathematical models. Its understanding aids in the development of more accurate and robust predictive models in diverse fields, driving innovation and improving decision-making processes.
Closing Insights: Summarizing the Core Discussion
The y-intercept is far more than just a point on a graph; it represents a crucial piece of information about the linear relationship it describes. Its value, combined with the slope, provides a complete picture of the line's behavior and allows for accurate predictions and analyses across a wide spectrum of applications.
Exploring the Connection Between the Slope and the Y-Intercept
The slope and the y-intercept work in tandem to define a linear relationship. The slope determines the steepness or inclination of the line, while the y-intercept determines where the line intersects the y-axis. Understanding the interplay between these two is key to fully grasping the characteristics of a linear equation.
Key Factors to Consider:
-
Roles and Real-World Examples: The slope represents the rate of change, while the y-intercept represents the initial value. In a sales context, the slope could represent the sales increase per month, and the y-intercept might represent initial sales at the start of the campaign.
-
Risks and Mitigations: Misinterpreting the y-intercept, especially in contexts where it doesn't have a direct physical meaning, can lead to inaccurate conclusions. Careful consideration of the context and units is crucial.
-
Impact and Implications: The combination of slope and y-intercept can significantly influence the prediction of future values. A steeper slope with a high y-intercept indicates faster growth, for instance.
Conclusion: Reinforcing the Connection
The interconnectedness of the slope and y-intercept is vital for a complete understanding of linear relationships. By carefully analyzing both parameters, we gain a holistic perspective on the data and can make informed interpretations and predictions.
Further Analysis: Examining the Slope in Greater Detail
The slope, often represented by 'm' in the equation y = mx + b, describes the rate of change between the dependent and independent variables. A positive slope indicates a positive correlation (as x increases, y increases), a negative slope indicates a negative correlation (as x increases, y decreases), and a zero slope indicates no correlation (y remains constant regardless of x). Understanding the slope's magnitude and sign is just as critical as understanding the y-intercept.
FAQ Section: Answering Common Questions About the Y-Intercept
-
What is the y-intercept? The y-intercept is the point where a line intersects the y-axis of a coordinate plane; its x-coordinate is always 0.
-
How do you find the y-intercept? Several methods exist: using the slope-intercept form, point-slope form, two-point form, or solving a system of equations.
-
What does the y-intercept represent? Its meaning depends on the context; it often represents an initial value, a starting point, or a fixed cost.
-
Can a line have more than one y-intercept? No, a straight line can only have one y-intercept.
-
What if the y-intercept is zero? This means the line passes through the origin (0,0).
Practical Tips: Maximizing the Benefits of Understanding the Y-Intercept
-
Visualize: Always graph the linear equation to visually confirm the y-intercept and its relationship to the slope.
-
Understand the Context: Carefully consider the meaning of the variables and the y-intercept within the specific application.
-
Check Your Work: Verify your calculations to ensure accuracy, especially in real-world applications where errors can have significant consequences.
Final Conclusion: Wrapping Up with Lasting Insights
The y-intercept, though a seemingly simple concept, is a powerful tool for understanding and analyzing linear relationships. Its importance extends beyond the classroom, finding applications in numerous fields. By mastering its definition, calculation methods, and interpretations, individuals can gain valuable insights and improve their analytical abilities in various contexts. A thorough understanding of the y-intercept, combined with an understanding of the slope, empowers informed decision-making and effective problem-solving across diverse disciplines.
Latest Posts
Latest Posts
-
How To Pass A Rental Credit Check For Free
Apr 04, 2025
-
How To Pass A Credit Score Check
Apr 04, 2025
-
How To Pass A Rental Credit Check Reddit
Apr 04, 2025
-
How To Pass A Soft Credit Check
Apr 04, 2025
-
How To Beat A Credit Check
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Definition Y Intercept . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.